Viele kombinatorische Optimierungsprobleme können äquivalent als lineare Programme formuliert werden, wobei man von einer Lösung zusätzlich Ganzzahligkeit verlangt. Die Zulässigkeitsbereiche sind dann nicht mehr Polyeder in Vektorräumen wie in der Linearen Optimierung, sondern ganzzahlige Gitter. Während nicht wenige dieser Probleme, die wie z.B. Netzwerkfluß- und Zuweisungsprobleme eine spezielle Struktur besitzen, effizient lösbar sind, ist das allgemeine ganzzahlige Optimierungsproblem schon im linearen Fall beweisbar schwierig (NP-vollständig).
Bisher ist kaum erforscht, wie man an dem zum Optimierungsproblem gehörigen Gitter ablesen kann, wie schwer das ganzzahlige lineare Programm zu lösen ist. Wir haben uns dieser Frage von zwei Seiten genähert.
Die Menge der 0-1-Vektoren eines GF(2)-Vektorraumes nennt man auch einen binären Code. In kombinatorischen Optimierungsproblemen tauchen diese vor allem als Menge der Zykel (geschlossenen Kantenzüge in einem Graphen) oder als Menge von Schnitten (Kantenmengen, deren Entfernung einen unzusammenhängenden Graphen entstehen läßt) oder allgemeiner als Kreisraum (``cycle space'') und Kokreisraum (``cocycle space'') binärer Matroide auf.
Das von solchen Vektoren erzeugte ganzzahlige Gitter spiegelt einerseits die steigende Komplexität des zugrundeliegenden Problems wieder, andererseits vermuten wir (zusammen mit Martin Loebl und Monique Laurent), daß diese Gitter im allgemeinen folgende bemerkenswerte Eigenschaft haben:
Dies ist ein Spezialfall einer noch allgemeineren Frage über Gitter, die von Delaunay-Polytopen erzeugt werden.
Diese Vermutung an sich widerstand bisher unseren Annäherungsversuchen. Allerdings haben wir inzwischen Gültigkeit in einigen Spezialfällen bewiesen und können außerdem nachweisen, daß kanonische Induktionsansätze, bei denen ein beliebiges Element kontrahiert oder gelöscht wird, zum Scheitern verurteilt sind.
Letzteres zeigen wir, indem wir die Äquivalenz unserer Vermutung zu einer Aussage über Untermatrizen von Hadamard-Matrizen vom Sylvester-Typ voller Zeilenlänge beweisen:
Die Spezialfälle, bei denen die Gültigkeit der Vermutung bekannt ist
(Resultate mit A. Gallucio, M. Loebl und M. Laurent), umfassen Kreise
und Schnitte in Graphen, Matroide vom Rang höchstens 4,
Kreise in projektiven Räumen, Matroide mit rekursiv monotoner
Struktur, reguläre Matroide, Grafts und Einpunkterweiterungen
von Matroiden ohne 
-Minor.
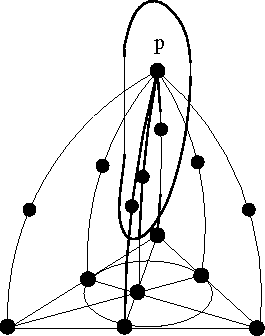
Abbildung: Kreisgitter projektiver Räume haben eine Basis aus Codewörtern.
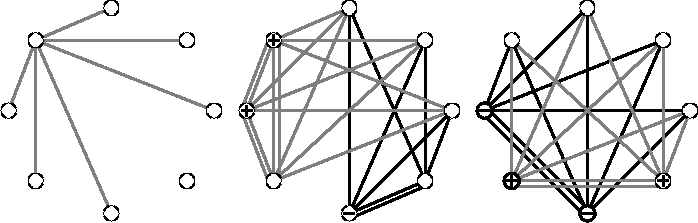
Abbildung: Repräsentanten der drei Klassen von Elementen in der
minimalen Testmenge für K
Conti und Traverso haben vor wenigen Jahren einen interessanten Zusammenhang zwischen ganzzahliger Optimierung und Gröbnerbasen in der kommutativen Algebra erkannt. Bei geeignet gewählter Formulierung einer Familie von beschränkten ganzzahligen Programmen läßt sich die Menge der zulässigen Lösungen mit einem Binomideal in einem Polynomring identifizieren. Legt man weiterhin eine bestimmte Monomordnung, die mit der Zielfunktion des Optimierungsproblems korrespondiert, auf dem Polynomring fest, so kann mit dem Buchberger-Algorithmus die Gröbnerbasis des Binomideals ausgerechnet werden. Der reduzierten Gröbnerbasis entspricht im Optimierungskontext die bezüglich Inklusion eindeutige minimale Testmenge, die durch folgende Eigenschaft charakterisiert ist: Eine zulässige Lösung x eines ganzzahligen Optimierungsproblems ist entweder optimal, oder es gibt ein Element t der Testmenge, so daß die Differenz x-t wieder zulässig ist und bezüglich der Zielfunktion einen besseren Wert hat.
Theoretisch besteht also die Möglichkeit, durch den Einsatz algebraischer Methoden ganzzahlige Optimierungsprobleme zu lösen: Erst wird mit dem Buchberger-Algorithmus die Testmenge ermittelt. Anschließend wird eine Folge von Verbesserungsschritten ,,entlang`` Elementen der Testmenge ausgeführt, bis das Optimum erreicht ist.
Obwohl in dem betrachteten Fall die Gröbnerbasis nur zu Idealen mit recht spezieller Struktur berechnet werden muß, ist dieser Ansatz aufgrund der hohen Laufzeit des Buchberger Algorithmus und der potentiell gewaltigen Größe der Basis für Beispiele mit vielen Variablen sehr problematisch. Daher werden die algebraischen Methoden nicht als direkte Lösungsverfahren betrachtet. Statt dessen werden die Methoden der Computeralgebra im hier verfolgten Ansatz dazu eingesetzt, die minimalen Testmengen zu ganzzahligen Optimierungsproblemen zu berechnen, um anschließend aus den so gewonnenen Informationen Aussagen über die Struktur der Testmengen zu ermöglichen.
Zunächst wurde anhand wohlbekannter kombinatorischer Optimierungsprobleme die Struktur entsprechender Gröbnerbasen studiert. So ist es beispielsweise im Falle der Bestimmung eines Matchings maximalen Gewichts in einem vollständig bipartiten Graphen gelungen, die Testmenge des dazu dualen Problems vollständig zu beschreiben, und zwar unabhängig von der Tatsache, daß zu ihrer Berechnung aufwendige algebraische Methoden eingesetzt wurden. Dieses Resultat scheint sich auf das gewichtete b-Matching-Problem übertragen zu lassen.
Weiterhin wurde ein Vertex-Cover-Problem auf vollständigen Graphen betrachtet. Bei geeigneter Wahl der Monomordnung gilt der
Satz: Bis auf ein Element ist die reduzierte Gröbnerbasis genau die Menge aller Vektoren, die entweder negativ bzgl. der Monomordnung sind und das Gewicht um 1 erniedrigen, oder das Gewicht unverändert lassen und positiv bzgl. der Ordnung sind.
In Abbildung 
sind typische Repräsentanten
der minimalen Testmenge für den K graphisch dargestellt.
Das linke Element und Elemente vom mittleren Typ erniedrigen das Gewicht
einer Knotenüberdeckung, während die Elemente vom rechten Typ
lediglich für eine Umverteilung der Gewichte stehen.
Ziel ist es, auch bei schweren ganzzahligen Optimierungsproblemen eine - möglicherweise unvollständige - Beschreibung der Struktur der Testmenge ermitteln zu können. Diese Kenntnisse können dann in einer Verbesserungsheuristik genutzt werden.